The next post in this series is here.
If you are into the latest language tech innovations, you very likely came across the notion of a neural network. You probably also heard of machine and deep learning. Maybe you are even considering a broader deployment of these technologies in your organization.
A Scientific Touch: An Introduction
To add a bit of an explanatory touch to our texts, we decided to cooperate with an expert in the matter – Mateusz Piorkowski from the University of Vienna – and start a mini-series, in which we explain scientific basics of those technologies in a clear and comprehensible manner.
These technologies will turn out to be closely related as well as fundamental to other, newer technologies, like computer vision or handwriting recognition. Some of these technologies are not really new, but they became more applicable due to increasing computational power.
So, what’s the master plan? First, we’ll explain what a Neural Network actually is, using a simple algorithm designed to recognize handwritten digits as an example. We’ll dive into their use of natural language processing, and further into neural machine translation. The purpose is to show you what is going on behind the curtain. Even if you are completely new to the subject!
So, What Is a Neuron?
For a start, let me explain just what a neuron is – it will be our main object of interest. At the moment, you can think of it as a small disk containing a number.
This number is not fixed but can change in time and in the future, we will omit the number from the drawings. Depending on the implementation, there might be some restriction on just what this value can be, for example, it is common to assume that it must be between 0 and 1.
In that case, you can think of a neuron with a value close to 0 as being inactive. Then, think of one with a value close to 1 as being active, with 0.5 being something in between. In general, we will call this number the ‘activation’ and denote it by ‘x’. In this case x = 0.31.
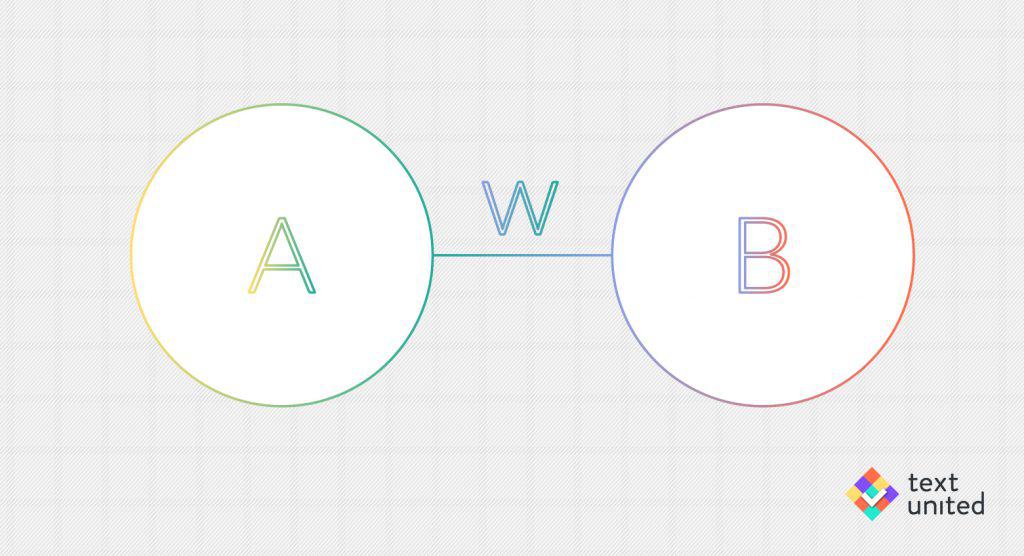
A neuron by itself will not take us very far. Just as in our brains, we need a lot of neurons that interact to get something interesting. Let’s start with two. We can schematically denote a connection with a line going from neuron A to neuron B.
The ‘w’ stands for ‘weight’ of a connection. It tells us how neuron B reacts to the activation of neuron A.
For example, if w = 2, then we should have something like XB = 2*XA (with XA, XB being the activation of neuron A, B respectively), hence the activation of neuron A would be amplified. There might be some problems if the activations are restricted to lie in some interval, like between 0 and 1. In that case something like XB = σ(w*XA) with σ a being a nonlinear function (nonlinear basically means that doubling the input will not necessarily double the output).
Let’s leave the details of what nonlinearity vs. linearity implies. For the purpose of this series, it is completely sufficient for you to know that a weight of a connection just dictates how one neuron reacts to another one.
Connections Are Important
The next step is to look at many neurons with many connections. A general structure of this type is called a ‘directed graph’. In fact, there is a separate mathematical field called ‘graph theory’. It quickly gains popularity among data scientist, biologists, and sociologists, fuelled by better algorithms and increasing computational power.
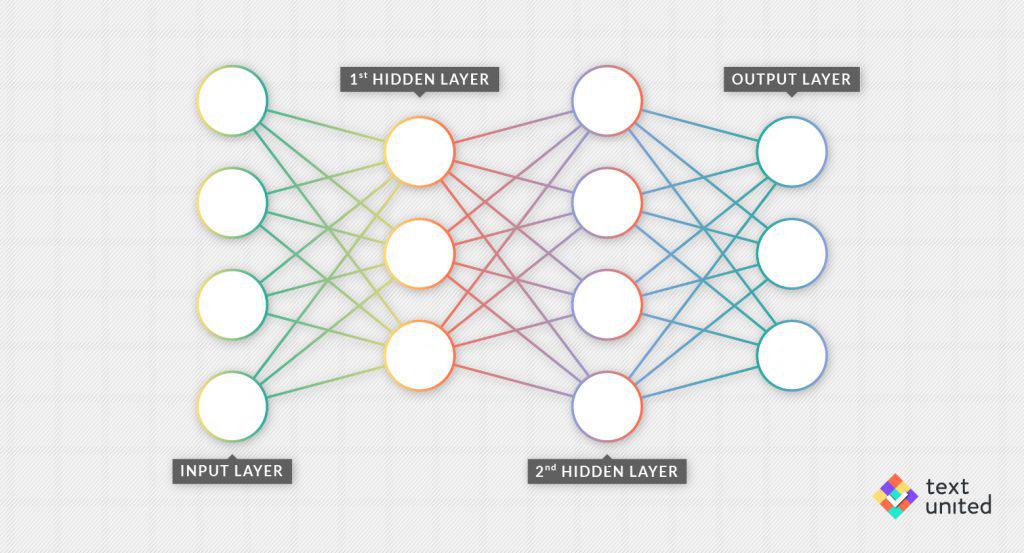
However, a general graph has too little structure for our purposes and so we need to introduce the concept of a ‘layer’. A layer is just a collection of neurons. Each of them is connected to every other in the preceding and next layer unless it is the input/output layer. The following picture should clear everything up:
Voila, we have a neural network!
Of course, there are many things the above picture does not tell us. For one, there is a huge amount of weights. We also have not specified some auxiliary assumptions about the neurons, like the nonlinear functions from the last paragraph.
However, we will just assume that everything has been chosen and initialized. Now you know the basics: what is a neuron and how do they connect. In part two of our series, we will go deeper and take a closer look at what a neural network really does.